Category:Polytopes
Jump to navigation
Jump to search
geometric object with flat sides | |||||
| Upload media | |||||
| Subclass of | |||||
|---|---|---|---|---|---|
| Has part(s) |
| ||||
| Different from | |||||
| |||||
العربية: في الهندسة الرياضية، يعرف متعدد الرؤوس أو بوليتوب على أنه تعميم لمصطلح مضلع في المستوي، متعدد السطوح في الفضاء الثلاثي الأبعاد، ولمصطلح بوليكورون في الفضاء الرباعي الأبعاد.
Deutsch: Polytop bezeichnet in der Geometrie ein verallgemeinertes Polygon in beliebiger Dimension. Man spricht von -Polytopen, wo die Dimension ist.
English: In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions (such as a polychoron in four dimensions). Some theories further generalise the idea to include such things as unbounded polytopes (apeirotopes and tessellations), and abstract polytopes.
Esperanto: En geometrio hiperpluredro estas ĝeneraligo al ĉiu dimensio de plurlatero en du dimensioj, pluredro en tri dimensioj, kaj plurĉelo en kvar dimensioj.
Español: En geometría politopo significa, en primer lugar, la generalización a cualquier dimensión de un polígono bidimensional, o un poliedro tridimensional. Además, este término es utilizado en varios conceptos matemáticos relacionados. Su uso es análogo al de cuadrado, que puede usarse para referirse a una región del plano de forma cuadrada, o sólo para sus límites, o aún para una mera lista de sus vértices y lados junto con alguna información acerca de la forma en que están conectados.
Français : Le terme polytope admet plusieurs définitions au sein des mathématiques. Principalement car les usages diffèrent en quelques points selon les pays, mais l'usage américain ayant tendance à s'imposer, on se retrouve confronté avec des usages contradictoires au sein d'un même pays. On retrouve ce genre de problème pour les définitions des faces et des facettes d'un polyèdre (pour un polyèdre de dimension n, Bourbaki définit les facettes comme les faces de dimension <n-1, le suffixe faisant penser à la petitesse, alors que les américains définissent une facette comme une face de dimension n-1, comme on dit en français d'ailleurs pour les facettes d'un diamant).
Italiano: Un politopo d-dimensionale o d-politopo è l'analogo di un poligono nel piano (d=2) e di un poliedro nello spazio usuale (d=3) generalizzato ad uno spazio euclideo reale . I poligoni si possono quindi anche chiamare 2-politopi e i poliedri 3-politopi. Il termine politopo è stato coniato da Alicia Boole, la figlia di George Boole.
Nederlands: Een Polytoop staat in de meetkunde voor een uitbreiding van het begrip polygoon in een gewenste dimensie. Net als de polygoon bestaat ook de polytoop uit meerdere punten in de ruimte, (hoekpunten) genaamd, die door ribben kunnen worden verbonden. Meerdere ribben omgeven de zijvlakken van een polytoop. De planaire polygonen van dimensie 2 zijn bijvoorbeeld het vierkant de (hexaëder) of een driehoek (tetraëder).
Polski: Wielokomórka (wielotop) to w geometrii uogólnienie na dowolną liczbę wymiarów pojęcia wielokąta w drugim i wielościanu w trzecim wymiarze.
Português: Em geometria, um polítopo é a generalização, para um número arbitrário de dimensões (finitas), dos conceitos de polígono e poliedro.
Русский: В геометрии политопом называется геометрический объект с плоскими гранями (сторонами), существующий в пространстве произвольной размерности. Многоугольник является двумерным политопом, многогранник — трёхмерным и т.п. Иногда к политопам относят также многогранники с бесконечным числом граней (апейротопы) и замощения.
Simple English: A polytope is figure in geometry. It is a generalisation of the polygon in two dimensions, and the polyhedron in 3 dimensions, to any number of dimensions.
Subcategories
This category has the following 34 subcategories, out of 34 total.
*
- 7-polytopes (1503 F)
- 9-polytopes (3 F)
- 10-polytopes (1 F)
A
C
- Compound polytopes (8 F)
D
G
H
L
N
O
P
R
- Realization maps (7 F)
S
U
V
W
- Wythoff construction (2 F)
Media in category "Polytopes"
The following 120 files are in this category, out of 120 total.
-
1 22 E6 to 3D H3 symmetry concentric hulls.png 741 × 591; 119 KB
-
1 22 polytope A4 Coxeter plane.png 1,443 × 1,491; 368 KB
-
120-cell-rotating-T-axis.gif 480 × 360; 9.69 MB
-
13-cube.svg 800 × 800; 3.43 MB
-
14-cube.svg 800 × 800; 7.33 MB
-
15-cube.svg 800 × 800; 14.83 MB
-
2-demicube graph.png 818 × 794; 11 KB
-
20 Ponted Cross Graph.svg 512 × 512; 22 KB
-
2D reflexive polytope.svg 135 × 135; 6 KB
-
3 21 E7 to 3D H3 symmetry concentric hulls.png 751 × 546; 108 KB
-
4 21 E8 to 3D H3 symmetry concentric hulls.png 594 × 853; 181 KB
-
4hosohedron.JPG 205 × 215; 8 KB
-
A view of Sir Isaac Newton's philosophy. Fleuron T053471-24.png 1,414 × 784; 69 KB
-
A4 Weyl Orbit 3D Convex Hulls.svg 1,581 × 3,484; 4 MB
-
Amorphic Polyhedron.png 228 × 219; 1 KB
-
Bidex projection.png 1,200 × 1,200; 838 KB
-
Biruncinatocubic honeycomb dual cell.png 573 × 573; 9 KB
-
Bitruncated tesseract stereographic.png 432 × 417; 119 KB
-
CD B4 nodes.png 37 × 25; 410 bytes
-
CD B4-nodes.svg 113 × 76; 5 KB
-
CD B5 nodes.png 51 × 27; 380 bytes
-
Circogoniaicosahedra ekw.jpg 157 × 175; 6 KB
-
Combined-Diagram-of-Special-Aspects-of-Mars-Saturn-and-Jupiter.png 809 × 612; 158 KB
-
Complex multipartite graph 16-cell.svg 1,000 × 1,000; 2 KB
-
ComplexOctagon.png 477 × 228; 6 KB
-
ComplexOctagon.svg 477 × 216; 45 KB
-
Cutting plane algorithm2.png 468 × 418; 7 KB
-
Cutting plane algorithm2.svg 990 × 765; 10 KB
-
D3InD3.svg 838 × 964; 43 KB
-
D4InD4.svg 826 × 826; 67 KB
-
D6-to-H3-edge.png 1,589 × 1,577; 2.34 MB
-
D6InD6.svg 937 × 937; 171 KB
-
D7inD7.svg 885 × 907; 259 KB
-
D8InD7Plane.svg 655 × 671; 376 KB
-
D8InD8.svg 837 × 837; 376 KB
-
DiamantUeberarbeiten.png 800 × 600; 346 KB
-
Dice analogy 0 to 5 dimensions.jpg 389 × 293; 28 KB
-
Dice analogy- 1 to 5 dimensions.svg 400 × 400; 5 KB
-
Dice analogy- 3 dimensions.svg 300 × 250; 797 bytes
-
Dice analogy- 4 dimensions.svg 375 × 325; 1 KB
-
Dice analogy- 5 dimensions.svg 400 × 400; 3 KB
-
Dodecadeltahedron-2.png 964 × 957; 105 KB
-
Dodecadeltahedron-2.svg 1,152 × 1,162; 436 bytes
-
Dodecadeltahedron.gif 548 × 544; 7 KB
-
Dodecagon representing 12 Zodiac signs.png 867 × 704; 38 KB
-
Dtp-3d 1.svg 300 × 300; 319 bytes
-
E6Coxeter.svg 599 × 599; 214 KB
-
E8 142-3D concentric hull list.png 1,574 × 7,917; 1.66 MB
-
E8 142-3D Concentric Hulls.png 1,161 × 2,571; 1.08 MB
-
E8 241-3D Concentric Hulls List.png 1,536 × 2,590; 404 KB
-
E8 241-3D Concentric Hulls.png 1,354 × 4,145; 861 KB
-
E8 241-3D.png 1,453 × 1,562; 568 KB
-
E8-3Dprint-b.png 419 × 419; 247 KB
-
E8-4D-Polychora.png 2,100 × 2,100; 7.14 MB
-
E8-6Cube.jpg 1,800 × 1,800; 745 KB
-
E8-6Cube.png 5,120 × 3,640; 1.61 MB
-
E8-F4mox.svg 512 × 512; 1,022 KB
-
E8rotation.theora.ogv 55 s, 600 × 600; 8.4 MB
-
Eutactic star.png 279 × 278; 2 KB
-
Example polytope graph TLR.png 600 × 599; 30 KB
-
Examples of polytopes as set of line segments.png 692 × 103; 2 KB
-
Expanded 2-simplex.png 662 × 687; 12 KB
-
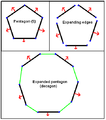
Expanding pentagon.png 474 × 536; 18 KB
-
F4Birectified.svg 512 × 512; 1.89 MB
-
F4Triality.svg 603 × 594; 3.21 MB
-
G2Coxeter.svg 590 × 512; 39 KB
-
GrandAntiPrism-2D-F4.svg 860 × 860; 191 KB
-
Hemitesseract-4-cells.png 1,437 × 1,449; 79 KB
-
Hemitesseract-graph.png 671 × 648; 24 KB
-
Hexacross.png 597 × 591; 220 KB
-
Hexagonal hosohedron.png 620 × 622; 24 KB
-
Hexagonal Hosohedron.svg 598 × 600; 9 KB
-
Hexagonale Kombination Prisma mit Rhomboeder.png 124 × 168; 16 KB
-
IP polytope with LP relaxation.png 844 × 699; 15 KB
-
IP polytope with LP relaxation.svg 500 × 415; 60 KB
-
Jupiter's-5th-Aspect.png 814 × 611; 121 KB
-
Jupiter's-9th-Aspect.png 770 × 628; 74 KB
-
Kreuzpolytop4d.png 403 × 397; 15 KB
-
Lineairprogrammeren2020091903.svg 512 × 529; 2 KB
-
Linear programming polytope.png 699 × 692; 18 KB
-
Linopt-feasible-region de.svg 411 × 444; 5 KB
-
Linopt-feasible-region.png 411 × 444; 7 KB
-
Linopt-feasible-region2.png 1,003 × 705; 17 KB
-
LisiE8.svg 416 × 419; 1.29 MB
-
Mars-4th-Aspect.png 800 × 671; 104 KB
-
Mars-8th-Aspect.png 837 × 638; 116 KB
-
Mike's Trihedron.PNG 469 × 206; 7 KB
-
N-wymiarowe sześciany.svg 700 × 864; 7 KB
-
Order-6 dodecahedral honeycomb.png 696 × 680; 688 KB
-
Penteractgif2222.gif 600 × 338; 10.43 MB
-
Polyhedron kaleidoscope triangles.png 779 × 455; 26 KB
-
Polytope model skewed.svg 1,100 × 550; 30 KB
-
Polytope model unskewed.svg 588 × 431; 26 KB
-
Prj20.svg 501 × 501; 231 KB
-
Prj24.svg 507 × 507; 231 KB
-
Proj20.svg 498 × 498; 2.97 MB
-
Proj20a.png 1,661 × 1,661; 2.26 MB
-
Proj24.svg 496 × 496; 2.97 MB
-
Proj24a.png 1,654 × 1,654; 2.2 MB
-
Pure 3-dimensional apeirohedra chart.png 1,023 × 366; 32 KB
-
Rectangular-tetron.png 324 × 212; 2 KB
-
Runcitruncated cubic honeycomb nets.svg 744 × 1,052; 58 KB
-
Simplex-Verfahren.jpg 1,000 × 847; 131 KB
-
Squarecubetesseract.png 1,957 × 640; 220 KB
-
Tetrahedral meet.png 787 × 739; 138 KB
-
The measurer's jewel Fleuron N034988-36.png 717 × 472; 14 KB
-
Tri-wedge-altitudes.png 632 × 368; 18 KB
-
Triangle-trion di-fusil.png 579 × 526; 38 KB
-
Triangle-trion di-meet.png 351 × 434; 6 KB
-
Triangle-trion di-wedge.png 579 × 526; 41 KB
-
Triangle-trion duoprism.png 351 × 434; 9 KB
-
Triangular wedge.png 585 × 642; 24 KB
-
Trion meet.png 623 × 765; 10 KB
-
Trion prism.png 629 × 783; 14 KB
-
Trion-diwedge.png 579 × 526; 40 KB
-
Trionic fusil.png 585 × 642; 22 KB
-
Trionic wedge.png 585 × 642; 22 KB
-
Uniform polytope 3,3,3,3,3,3 t0.jpg 4,608 × 3,456; 3.25 MB