Spherical harmonic
Appearance
Let us consider continuous functions that only depend on the orientation in space (θ,φ). The spherical harmonics are a basis of such functions.
The decomposition in spherical harmonics is used to represent these functions ; it is similar to the Fourier transform for periodic functions.
In the plane (circular harmonics)
[edit]A function is decomposed as
where Yl is the circular harmonic. It is expressed as
where Pl is the Legendre polynomial
The circular harmonics are represented in three ways:
- in cartesian coordinates:
- in polar coordinates:
- in polar coordinates:
| Cartesian plot of | Polar plot of | Polar plot of | |
|---|---|---|---|
| 1 | 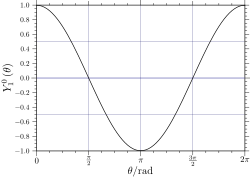
|

|

|
| 2 | 
|

|

|
| 3 | 
|

|
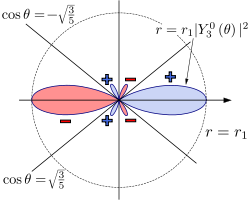
|
| 4 | 
|
In space
[edit]| m=0 | m=1 | m=2 | m=3 | m=4 | |
|---|---|---|---|---|---|
| l=0 | |||||
| l=1 | |||||
| l=2 | |||||
| l=3 | |||||
| l=4 |
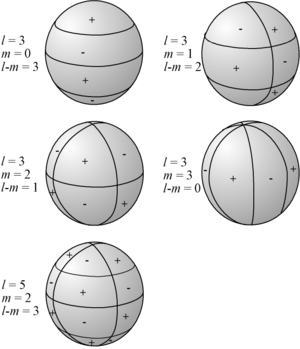
then the representative surface looks like a "battered" sphere;
Ylm is equal to 0 along circles (the representative surface intersects the ρ = ρ0 sphere at these circles). Ylm is alternatively positive and negative between two circles.










