Help:SVG for math
This article presents several techniques to prepare SVG plots for math use. We will discuss some math topics that demand extensive vector plots, as well as some useful programs for preparation. For SVG in general topics, see help:SVG.
Motivation
[edit]The requirement of accuracy in math works significantly contributes to the high demand of vector plotting. Clearly SVG is one of the most popular vector image formats. Most Wikipedia vector images are in SVG. There are many programs (Gnuplot, Matplotlib, R, LaTeX, Inkscape, etc.) that can help prepare SVG images. A considerably large proportion of the programs are math-oriented. On the other hand, there are many branches (category theory, statistics, dynamical systems, etc.) that require extensive vector plots. It is definitely doable to give a vector plot in order to address a math conception (i.e., the construction of a category), or show a solution (i.e., the pdf and cdf of a probability distribution).
Currently on Wikipedia, there is quite a large space for improvement on math SVG plots. One can easily find many bitmaps (most are in PNG) in the math related articles. Most of these bitmaps can be better presented in a vector plot. One may retouch the plots in SVG format by using some programs (most are freewares). Hence it is appropriate to summarize the tips for SVG plot preparation.
Math Topics that Favor Vector Plots
[edit]In this section we will discuss several math topics in which vector plots are frequently used. We give typical examples for each topic. One may be interested in some of these topics and contribute vector graphics, if any.
Dynamical Systems
[edit]The plots in dynamical systems include the solutions to the differential equations, the orbits in the phase space, numerical simulation of the differential system, etc.
Solutions to Differential Equations
[edit]
The plot above gives the solutions of the following differential equations under different initial conditions.[1]
The solutions to this differential system have simple closed forms. Hence the plotting program only needs routine computations. As a result, one may use Gnuplot for this case. To plot the multiple curves in the graph, we can leverage the for loop in Gnuplot (version 4.4+ required). This technique can also produce the plots of some elementary functions (exponential, logarithm, etc.).
Unfortunately most differential equations have complicated solutions that cannot have closed forms. For this scenario, one may choose Matplotlib or MATLAB rather than Gnuplot, since Gnuplot is not very good at complicated computation, and Matplotlib and MATLAB can make advanced computations in an accessible way.
Trajectories in Phase Spaces
[edit]
The plot above gives the orbit of a limit cycle in the phase space. This plot requires extensive numerical computations. Hence Matplotlib, MATLAB and Mathematica can do this job. Among them Matplotlib is the most popular in Wikipedia since it is free. Here Gnuplot may not be very useful since it can only simply compute. If one chooses to plot by using Gnuplot for this case, he has to give how to obtain the data file, if any. For example, one asks Gnuplot to give the plot based on an exterior data file:
plot "foo.dat" using 1:2 title 'foo'
Here the data file foo.dat should be provided. One may directly upload the original data file, or give the generating source code.
Numerical Simulation
[edit]
The plot above numerically simulates the solution to the planar Navier-Stokes equation of the obstructed duct problem. The program leverages some advanced mathematical techniques. Thus it will be very beneficial for the readers and future developers if the author can leave a brief introduction to the solution idea. By doing this we can significantly relieve the pain of code reading. This plot needs a 3-dimensional representation and it requires a large amount of computation. Hence one may use Matplotlib or MATLAB to plot this image.
Probability and Statistics
[edit]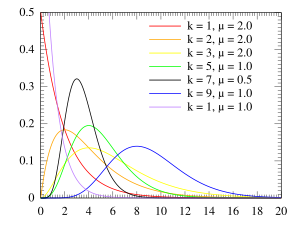
The plot above gives the pdf of Erlang distribution. Since most probability distributions have closed forms in which some special functions (i.e., Gamma function, Beta function) may be used, we favor Gnuplot. Some distributions (i.e., Gamma distribution, F distribution) have diverse shapes for various parameters. Correspondingly one may use the for loop in Gnuplot 4.4+ to draw multiple curves. To prepare a joint bivariate distribution, 3-dimensional representation is appropriate. Then one may use the 3D axes plotting in Gnuplot [2].
To prepare the plots of probability distributions, one may also use the software R, which is extensively used in statistics.
Homological Algebra and Category Theory
[edit]
The plot above gives the construction of Snake lemma in homological algebra and category theory, both of which have extensive uses on commutative diagrams. To prepare the diagrams, LaTeX must be the first choice, since most existing literatures use LaTeX to typeset. To adjust the page size, one may use the package geometry, or manually edit by using Inkscape. Since most LaTeX distributions cannot produce SVG files directly,[3] one may use some other programs (i.e., PDF2SVG) to transform the output files (i.e., PDF files) into SVG ones. Similarly it is a good practice to give LaTeX code for the future edits.
Without uploading an SVG file, one may barely use LaTeX commands to produce the commutative diagrams like what nLab does. By doing this it will be very convenient for the future revisions. However it may significantly reduce the elegancy. For example, is an alternative for the diagram  .
.
Common Programs to Prepare SVG for Wikipedia
[edit]This sections presents several frequently used freewares to generate vector images within the community of Wikipedia. Each program has its own particular advantages within a certain area and thus one may make a careful choice before plotting.
LaTeX
[edit]As an important typesetting system in math, LaTeX produces decent vector plots. One may use LaTeX to plot procedural graphics [4]. LaTeX has offered many packages (i.e., Xy-pic, PGF/TikZ, PSTricks) to plot vector images. Among them, Xy-pic is the most frequently used package when drawing commutative diagrams [5]. For some simple manual plotting, one may also use the LaTeX plot instructions. By doing this it can maximally preserve the elegancy of procedural graphics. For very complex plots, plotting in LaTeX way may incur very long code, which is difficult to read. To address this problem, we may choose Inkscape instead.
Gnuplot
[edit]Gnuplot can be used to draw most 2 or 3 dimensional function plots, histograms and coordinate charts. Gnuplot can produce decent SVG graphics and one may directly upload the generated images without further revision. Also we encourage the uploader to share the source code.
The most significant disadvantage of Gnuplot is its lack of advanced computation capacity. If your plot program contains a complex iterative/recursive algorithm, Gnuplot can hardly achieve the goal. Usually we accomplish the goal by using pipe in Gnuplot to invoke some exterior programs (i.e., awk). Sometimes the plot can also be done without pre-processing, but the incurred source code can be less readable [6].
Matplotlib
[edit]Matplotlib is a free but also powerful alternative of MATLAB. If the plot plan contains complicated computations or heavily iterative algorithms, one may choose Matplotlib by leveraging the power of computer programming.
To master Matplotlib, one has to get familiar with the programming language Python firstly.
R
[edit]R is an open source statistical software. It can produce statistical plots (i.e., probability distributions, bar charts, regression plots) with high quality. Many statisticians also use SAS. Both R and SAS well support SVG [7] [8]. Hence R may be the first choice within the statistical scope.
Inkscape
[edit]Inkscape is a popular SVG editor focusing on manual plotting. It can deal with some complex plots that are difficult to generate by solely running LaTeX programs. Inkscape can also work together with other programs. For example, some Gnuplot distributions fail to process the Greek symbols in a proper way (i.e., α will be a) [9]. To address this problem, one may use Inkscape to directly edit the output SVG file of Gnuplot. Usually the final version edited by Inkscape can be rendered correctly by Wikipedia.
By using Inkscape, one may also directly trace the bitmaps and output SVG versions. Be careful since in this way the output SVG file may be unnecessarily large.
Miscellaneous
[edit]

- For the plots generated by programs, it will be much more convenient for the future edits if one leaves the program source code after uploading the vector images. Usually it is extremely difficult to reproduce the plot in an exactly identical way without the original source code.
- Clearly editing SVG by using plain text editors (i.e., Vim, Emacs, Notepad++) can produce elegant and light weighted images. However, for the math plots which require extensive computations, hardcoding[10] the numerical results in the SVG file will increase the difficulty for the future edits. To solve this problem, one may briefly give comments before the computer-generated data set in the SVG file (i.e., the program source code that generates the data set, the compilation instructions). In fact, most users (not computer experts) prefer to directly revise the source code of the generating program, rather than delve into the SVG tags.
References
[edit]- ↑ Here v0 is the constant initial velocity. The initial angle θ can take different values.
- ↑ A brief introduction to Gnuplot 3-dimensional plotting: [1]
- ↑ Most LaTeX distributions can easily generate DVI, PS and PDF files.
- ↑ For more details, please see the chapter Creating Graphics in the LaTeX Wikibook.
- ↑ Xy-pics user guide by the University of British Columbia
- ↑ Gnuplot has limited capacity in data processing. Here is an example.
- ↑ R documentation
- ↑ SAS/GRAPH 9.2 documentation, 2nd edition
- ↑ See Guidelines in w:Wikipedia:How_to_create_charts_for_Wikipedia_articles.
- ↑ What is hardcoding?


