Hasse diagram
Jump to navigation
Jump to search
Misc.
[edit] Subsets of a 2-element set |
 Subsets of a 3-element set |
 Divisors of 60 ordered by divisibility |
 Non-negative integers ordered by divisibility | ||||||||
 Young–Fibonacci lattice |
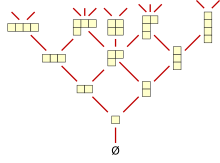 Young's lattice |
 Left: Divisors of 120 ordered by divisibility (Birkhoff's representation theorem) | |||||||||
 Associahedron of order 4 |
 Permutohedron of order 4 |
 Lattice of regular bands | |||||||||
 Free distributive lattices of monotonic Boolean functions |
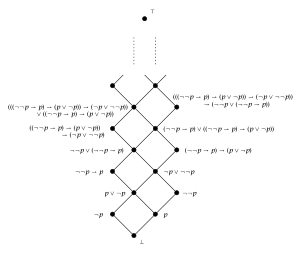 Rieger–Nishimura lattice (free Heyting algebra over one generator) |
 Types of quadrilaterals | |||||||||
Subsets of a 4-element set:
 Emphasis on two cubes |
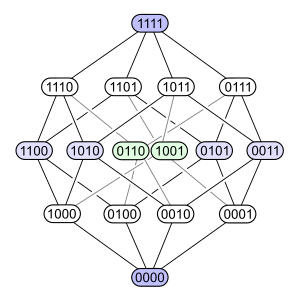 Rhombic dodecahedral parallel projection of the tesseract |
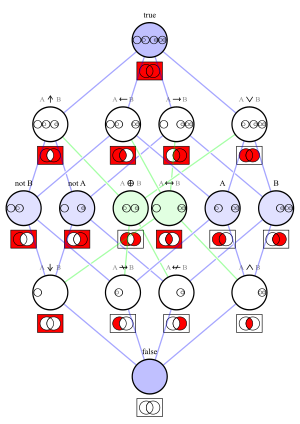 Logical connectives |
 Emphasis on all eight cubes |
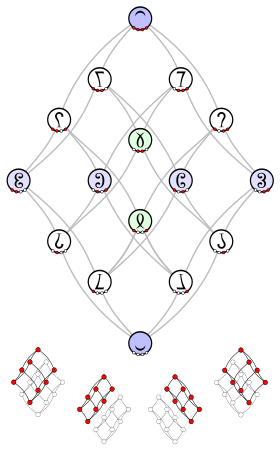 4x4 matrix |
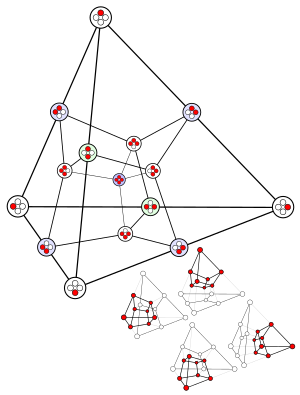 Tetrahedral central projection of the tesseract Not a Hasse diagram, but similar: Highest element in center; lower elements farer away from center; lowest element not shown |
Partitions of a 4-element set ordered by refinement:
 |
 |
 Only the 14 noncrossing partitions (This diagram is also vertically symmetric.) |
 Emphasis on sublattice |
 Emphasis on symmetry |
 Emphasis on number of elements per rank |
 Dihedral group Dih4 |
 Z23 |
 Z24 (rank expressed by background color, not by position) |
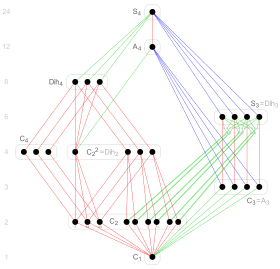 30 subgroups of S4 |
 9 types of subgroups of S4 |
 25 types of subgroups of the S4 × C2 |

|

|

|

|

|
 A7 |
 C5 |
 F4 |