File:Sampling the Discrete-time Fourier transform.svg

From Wikimedia Commons, the free media repository
Jump to navigation Jump to search

Original file (SVG file, nominally 754 × 562 pixels, file size: 46 KB)

Captions

Captions

Add a one-line explanation of what this file represents

Summary

[edit]
Description
English: Definitions: DTFT=discrete-time Fourier transform; DFT=discrete Fourier transform

Nine symmetric samples of a cosine function are shifted from the finite Fourier transform domain [-4,4] to the DFT domain [0,8], causing its DTFT to become complex-valued, except at the frequencies of an 8-length DFT. Pictured here are the real and imaginary parts of the DTFT after the cosine is multiplied by a symmetric Gaussian window function. Also shown (in red) are the estimates obtained by deleting the 9th data sample (equivalent to applying an 8-length DFT-even (aka periodic) window) and performing an 8-length DFT. The imaginary parts of the estimates exactly match the zero-valued DTFT function, which Harris[1] attributes to "DFT-even symmetry". But the real parts have a negative bias. Increasing the gain of the window function (the sum of its coefficients) improves the one positive-value estimate, but degrades the four negative ones.

The exact way to compute the estimates with an 8-length DFT is to combine the first and last samples by addition (instead of truncation), called periodic summation, with period 8. Then the outcomes (blue circles) exactly match the DTFT graphs.
Date
Source Own work
Author Bob K
Permission
(Reusing this file)
I, the copyright holder of this work, hereby publish it under the following license:
Creative Commons CC-Zero This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication.
The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.

Other versions Also see File:Comparison_of_symmetric_and_periodic_Gaussian_windows.svg.
Usage
InfoField
Additional information can be found at Window_function#DFT-symmetry. And Sampling the DTFT links to this image.
SVG development
InfoField
 
The source code of this SVG is invalid due to an error.
V
 
This W3C-invalid vector image was created with GNU Octave.
Gnu Octave source
InfoField
click to expand

This graphic was created by the following Octave script: 

pkg load signal
graphics_toolkit gnuplot
%=======================================================
function out=gauss(M2,sigma)     % window function
out = exp(-.5*(((0:M2)-M2/2)/(sigma*M2/2)).^2);
endfunction
%=======================================================
% Dimensions of figure
  x1 = .07;                     % left margin
  x2 = .02;                     % right margin
  y1 = .07;                     % bottom margin for annotation
  y2 = .07;                     % top margin for title

  width = 1-x1-x2;
  height= 1-y1-y2;

  x_origin = x1;
  y_origin = 1;                 % start at top of graph area
%=======================================================
set(0, "DefaultAxesFontsize",12)
set(0, "DefaultTextFontsize",14)
figure("position",[50 100 800 600]);

y_origin = y_origin -y2 -height;        % position of top row
subplot("position",[x_origin y_origin width height])

N   = 8*9*10;
M   = 4;                                % finite Fourier transform domain is [-M,M]
M2  = 2*M;
M21 = M2+1;                             % sequence length
symmetric = gauss(M2,1);
symmetric = symmetric/sum(symmetric);
periodic  = symmetric(1:M2);
periodic  = periodic/sum(periodic);

% A similar window is:
% window = kaiser(M21+2, pi*.75)';
% window = window(2:end-1);  % Remove zero-valued end points

x = 0:M2;
y      = cos(2*pi*x/4);
y_sym  = y.*symmetric;
y_even = y(1:end-1).*periodic;

DTFT    = fft(y_sym,N);
DFT     = fft([y_sym(1)+y_sym(end) y_sym(2:end-1)]); % periodic summation
DFTeven = fft(y_even);                               % truncation (aka "DFT-even")

x = 0:N/2;
plot(x, real(DTFT(1+x)), "color","blue")
hold on
plot(x, imag(DTFT(1+x)), "color","blue", "linestyle","--")
set(gca, "xaxislocation","origin")
xlim([0 N/2])
ylim([-0.4 0.6])

x = (0:M);
DFT     = DFT(1+x);
DFTeven = DFTeven(1+x);
x = x*N/M2;
plot(x, real(DFT),     "color","blue", "o", "markersize",8, "linewidth",2)
plot(x, real(DFTeven), "color","red",  "*", "markersize",4, "linewidth",2)
plot(x, imag(DFT),     "color","blue", "o", "markersize",8, "linewidth",2)
plot(x, imag(DFTeven), "color","red",  "*", "markersize",4, "linewidth",2)

h = legend("DTFT real",...
           "DTFT imaginary",...
           "periodic summation",...
           "DFT-even (truncation)", "location","northeast");
set(h, "fontsize",10)
%legend boxoff

set(gca, "xtick", x, "xgrid","on", "xticklabel",[0 1 2 3 4])
xlabel("DFT bins", "fontsize",14)
ylabel("amplitude")
title("Sampling the Discrete-time Fourier transform", "fontsize",14);
References
InfoField
  1. ↑ Harris, Fredric J. (1978-01). "On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform". Proceedings of the IEEE 66 (1): 52. DOI:10.1109/PROC.1978.10837.
  2. Sampling the DTFT

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current16:02, 19 August 2020Thumbnail for version as of 16:02, 19 August 2020754 × 562 (46 KB)Bob K (talk | contribs)make some objects darker
13:49, 19 August 2020Thumbnail for version as of 13:49, 19 August 2020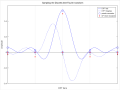754 × 562 (53 KB)Bob K (talk | contribs)Normalize DFT-even window coefficients. Change graph symbols.
13:32, 28 March 2020Thumbnail for version as of 13:32, 28 March 2020754 × 562 (47 KB)Bob K (talk | contribs)replace Hamming with a Gaussian to emphasize the difference between summation and truncation
16:06, 25 March 2020Thumbnail for version as of 16:06, 25 March 2020754 × 562 (41 KB)Bob K (talk | contribs)Uploaded own work with UploadWizard

You cannot overwrite this file.

There are no pages that use this file.

Metadata

This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.

Retrieved from "https://commons.wikimedia.org/w/index.php?title=File:Sampling_the_Discrete-time_Fourier_transform.svg&oldid=893636634"