File:NonConvex.gif
From Wikimedia Commons, the free media repository
Jump to navigation
Jump to search
NonConvex.gif (360 × 392 pixels, file size: 782 KB, MIME type: image/gif, looped, 84 frames, 4.2 s)
File information
Structured data
Captions
Captions
Add a one-line explanation of what this file represents
Summary
[edit]| DescriptionNonConvex.gif |
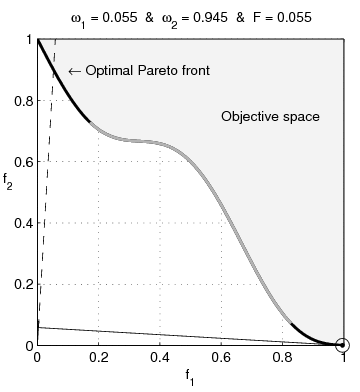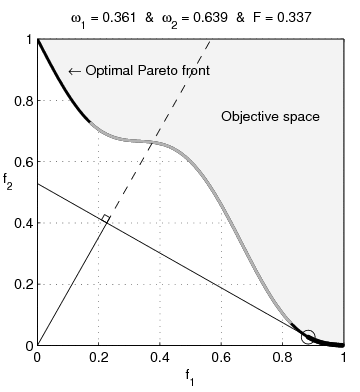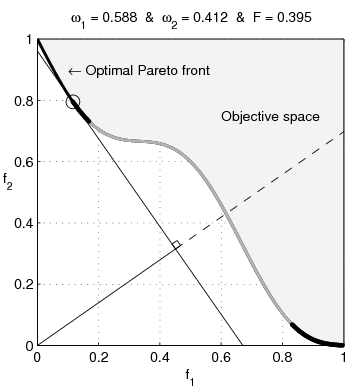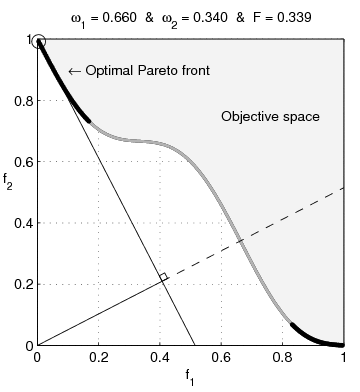
English: Weighted-sum approach is an easy method used to solve multi-objective optimization problem. It consists in aggregating the different optimization functions in a single function. However, this method only allows to find the supported solutions of the problem (i.e. points on the convex hull of the objective set). This animation shows that when the outcome set is not convex, not all efficient solutions can be found
Français : La méthode des sommes pondérées est une méthode simple pour résoudre des problèmes d'optimisation multi-objectif. Elle consiste à aggréger l'ensemble des fonctions dans une seule fonction avec différents poids. Toutefois, cette méthode permet uniquement de trouver les solutions supportées (càd les points non-dominés appartenant à l'enveloppe convexe de l'espace d'arrivée). Cette animation montre qu'il n'est pas possible d'identifier toutes les solutions efficaces lorsque l'espace d'arrivée est n'est pas convexe. |
| Date | |
| Source | Own work |
| Author | Guillaume Jacquenot |
function MO_Animate(varargin)
% This function generates objective space images showing why
% sum-weighted optimizer can not find all non-dominated
% solutions for non convex objective spaces in multi-ojective
% optimization
%
% Guillaume JACQUENOT
if nargin == 0
% Simu = 'Convex';
Simu = 'NonConvex';
save_pictures = true;
interpreter = 'none';
end
switch Simu
case 'NonConvex'
a = 0.1;
b = 3;
stepX = 1/200;
stepY = 1/200;
case 'Convex'
a = 0.2;
b = 1;
stepX = 1/200;
stepY = 1/200;
end
[X,Y] = meshgrid( 0:stepX:1,-2:stepY:2);
F1 = X;
F2 = 1+Y.^2-X-a*sin(b*pi*X);
figure;
grid on;
hold on;
box on;
axis square;
set(gca,'xtick',0:0.2:1);
set(gca,'ytick',0:0.2:1);
Ttr = get(gca,'XTickLabel');
Ttr(1,:)='0.0';
Ttr(end,:)='1.0';
set(gca,'XTickLabel',[repmat(' ',size(Ttr,1),1) Ttr]);
Ttr = get(gca,'YTickLabel');
Ttr(1,:)='0.0';
Ttr(end,:)='1.0';
set(gca,'YTickLabel',[repmat(' ',size(Ttr,1),1) Ttr]);
if strcmp(interpreter,'none')
xlabel('f1','Interpreter','none');
ylabel('f2','Interpreter','none','rotation',0);
else
xlabel('f_1','Interpreter','Tex');
ylabel('f_2','Interpreter','Tex','rotation',0);
end
set(gcf,'Units','centimeters')
set(gcf,'OuterPosition',[3 3 3+6 3+6])
set(gcf,'PaperPositionMode','auto')
[minF2,minF2_index] = min(F2);
minF2_index = minF2_index + (0:numel(minF2_index)-1)*size(X,1);
O1 = F1(minF2_index)';
O2 = minF2';
[pF,Pareto]=prtp([O1,O2]);
fill([O1( Pareto);1],[O2( Pareto);1],repmat(0.95,1,3));
text(0.45,0.75,'Objective space');
text(0.1,0.9,'\leftarrow Optimal Pareto front','Interpreter','TeX');
plot(O1( Pareto),O2( Pareto),'k-','LineWidth',2);
plot(O1(~Pareto),O2(~Pareto),'.','color',[1 1 1]*0.8);
V1 = O1( Pareto); V1 = V1(end:-1:1);
V2 = O2( Pareto); V2 = V2(end:-1:1);
O1P = O1( Pareto);
O2P = O2( Pareto);
O1PC = [O1P;max(O1P)];
O2PC = [O2P;max(O2P)];
ConvH = convhull(O1PC,O2PC);
ConvH(ConvH==numel(O2PC))=[];
c = setdiff(1:numel(O1P), ConvH);
% Non convex
O1PNC = O1PC(c);
[temp, I1] = min(O1PNC);
[temp, I2] = max(O1PNC);
if ~isempty(I1) && ~isempty(I2)
plot(O1PC(c),O2PC(c),'-','color',[1 1 1]*0.7,'LineWidth',2);
end
p1 = (V2(1)-V2(2))/(V1(1)-V1(2));
hp = plot([0 1],[p1*(-V1(1))+V2(1) p1*(1-V1(1))+V2(1)]);
delete(hp);
Histo_X = [];
Histo_Y = [];
coeff = 0.02;
Sq1 = coeff *[0 1 1 0 0;0 0 1 1 0];
compt = 1;
for i = 2:1:length(V1)-1
if ismember(i,ConvH)
p1 = (V2(i+1)-V2(i-1))/(V1(i+1)-V1(i-1));
x_inter = 1/(1+p1^2)*(p1^2*V1(i)-p1*V2(i));
hp1 = plot([0 1],[p1*(-V1(i))+V2(i) p1*(1-V1(i))+V2(i)],'k');
% hp2 = plot([x_inter],[-x_inter/p1],'k','Marker','.','MarkerSize',8)
hp3 = plot([0 x_inter],[0 -x_inter/p1],'k-');
hp4 = plot([x_inter 1],[-x_inter/p1 -1/p1],'k--');
hp5 = plot(V1(i),V2(i),'ko','MarkerSize',10);
% Plot the square for perpendicular lines
alpha = atan(-1/p1);
Mrot = [cos(alpha) -sin(alpha);sin(alpha) cos(alpha)];
Sq_plot = repmat([x_inter;-x_inter/p1],1,5) + Mrot * Sq1;
hp7 = plot(Sq_plot(1,:),Sq_plot(2,:),'k-');
Histo_X = [Histo_X V1(i)];
Histo_Y = [Histo_Y V2(i)];
hp6 = plot(Histo_X,Histo_Y,'k.','MarkerSize',10);
w1 = p1/(p1-1);
w2 = 1-w1;
Fweight_sum = V1(i)*w1+w2*V2(i);
Fweight_sum = floor(1e3*Fweight_sum )/1e3;
w1 = floor(1000*w1)/1e3;
str1 = sprintf('%.3f',w1);
str2 = sprintf('%.3f',1-w1);
str3 = sprintf('%.3f',Fweight_sum);
if (strcmp(str1,'0.500')||strcmp(str1,'0,500')) && strcmp(Simu,'NonConvex')
disp('Two solutions');
end
title(['\omega_1 = ' str1 ' & \omega_2 = ' str2 ' & F = ' str3],'Interpreter','TeX');
axis([0 1 0 1]);
file = ['Frame' num2str(1000+compt)];
if save_pictures
saveas(gcf, file, 'epsc');
end
compt = compt +1;
pause(0.001);
delete(hp1);
delete(hp3);
delete(hp4);
delete(hp5);
delete(hp6);
delete(hp7);
end
end
disp(['Number of frames :' num2str(length(V1))]);
return;
function [A varargout]=prtp(B)
% Let Fi(X), i=1...n, are objective functions
% for minimization.
% A point X* is said to be Pareto optimal one
% if there is no X such that Fi(X)<=Fi(X*) for
% all i=1...n, with at least one strict inequality.
% A=prtp(B),
% B - m x n input matrix: B=
% [F1(X1) F2(X1) ... Fn(X1);
% F1(X2) F2(X2) ... Fn(X2);
% .......................
% F1(Xm) F2(Xm) ... Fn(Xm)]
% A - an output matrix with rows which are Pareto
% points (rows) of input matrix B.
% [A,b]=prtp(B). b is a vector which contains serial
% numbers of matrix B Pareto points (rows).
% Example.
% B=[0 1 2; 1 2 3; 3 2 1; 4 0 2; 2 2 1;...
% 1 1 2; 2 1 1; 0 2 2];
% [A b]=prtp(B)
% A =
% 0 1 2
% 4 0 2
% 2 2 1
% b =
% 1 4 7
A=[]; varargout{1}=[];
sz1=size(B,1);
jj=0; kk(sz1)=0;
c(sz1,size(B,2))=0;
bb=c;
for k=1:sz1
j=0;
ak=B(k,:);
for i=1:sz1
if i~=k
j=j+1;
bb(j,:)=ak-B(i,:);
end
end
if any(bb(1:j,:)'<0)
jj=jj+1;
c(jj,:)=ak;
kk(jj)=k;
end
end
if jj
A=c(1:jj,:);
varargout{1}=kk(1:jj);
else
warning([mfilename ':w0'],...
'There are no Pareto points. The result is an empty matrix.')
end
return;
The weighted-sum approach minimizes function 

where


such that


To have a non-convex outcome set, parameters 



Weights 


![{\displaystyle \omega _{1}\in [0;1]~}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99c8913e84daf282e85b04849cc18cc14594dda7)

This diagram was created with MATLAB.
Licensing
[edit]I, the copyright holder of this work, hereby publish it under the following licenses:

|
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
You may select the license of your choice.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:13, 8 March 2009 |  | 360 × 392 (782 KB) | Gjacquenot (talk | contribs) | {{Information |Description={{en|1=Weighted-sum approach is an easy method used to solve multi-objective optimization problem. It consists in aggregating the different optimization functions in a single function. However, this method only allows to find th |
You cannot overwrite this file.
File usage on Commons
There are no pages that use this file.
File usage on other wikis
The following other wikis use this file:
- Usage on ar.wikipedia.org
- Usage on az.wikipedia.org
- Usage on de.wikipedia.org
- Usage on el.wikipedia.org
- Usage on en.wikipedia.org
- Usage on pt.wikipedia.org
- Usage on ru.wikipedia.org
- Usage on sr.wikipedia.org
- Usage on zh.wikipedia.org