Category:Tesseract subspaces (image set)

 See also categories: Cube subspaces (image set) and Face lattice of the tesseract (Bilinski).

These are the sets of fixed points of permutations of the tesseract, i.e. mainly its equivalents of symmetry axes and mirror planes,
which have 1, 2, and 3 dimensions (plus the origin and the whole space as least and greatest elements).

Their total number is 116. That is entry 4 of  A007405, the Dowling numbers.
Their number by dimension is row 4 of  A039755, the B-analogs of Stirling numbers of the second kind.

Permutations corresponding to the 12 types of subspaces
It can be seen, that the permutations have the same parity as the dimension of the subspace. Odd permutations are those in the slightly darker squares (with an odd number in it). Compare: Tesseract subspaces; permutations in 24×16 matrix
All permutations for each type of subspace a b c d 4 1 3 4 12 2 6 + 12 = 18 24 12 32 1 4 + 24 + 32 = 60 12 + 24 = 36 32 48 0 1 + 12 + 12 + 32 + 48 = 105 Permutations for one example subspace of each type There are five types of subspace, where only one permutation corresponds to each subspace. The matrices in the right half of the table are those without a unique self-inverse permutation. (E.g. 2d are rotations by 1/3.) a b c d 4   3     2     1 0

Example: Some subspaces of cuboid 3b11
	3b11 1, 3,   2, 4, 36,   35, 37, 33, 39,   32, 34, 38, 40
	2a0 1, 3,   2, 4	2b17 1,   36,   35, 37	2c11 4, 36,   32, 40	2d15 1,   39,   38, 40
	1a0 1	1b11 36	1c15 39	1d7 40
Tesseract face centers and their integer values from −40 to 40	Subspaces and the positive integers of the face centers they contain

Nested in the following collapsible tables are projections of all 116 subspaces together with a list of the positive face centers they contain.
The balanced ternary coordinates suggest a tesseract with ±1 vertex coordinates, i.e. with edge length 2. Anyway, the lengths mentioned below refer to a tesseract with edge length 1.

Each subspace is the set of fixed points of at least one permutation. If there is more than one, they are shown in a 16×24 matrix.

76 subspaces of 9 types have a unique self-inverse permutation. The pair ${\displaystyle (m,n)}$ of this permutation is shown next to the projection of the subspace.
The self-inverse permutation is unique (e.g. a 180° rotation), but there can be other permutations with the same set of fixed points (e.g. two 90° rotations).

The tesseract contains all of the 81 face centers. So its set of positive face centers is the whole list from ${\displaystyle 1}$ to ${\displaystyle 40}$. Only the neutral permutation leaves the whole tesseract unchanged.    00

(4, 12, 16, 8): [ 
    (1, 3, 9, 27, 2, 4, 8, 10, 6, 12, 26, 28, 24, 30, 18, 36, 5, 7, 11, 13, 23, 25, 29, 31, 17, 19, 35, 37, 15, 21, 33, 39, 14, 16, 20, 22, 32, 34, 38, 40)
]

3a 4 cubes with edge length ${\displaystyle 1}$ (green)    00
list (3, 6, 4, 0): [ (1, 3, 9, 2, 4, 8, 10, 6, 12, 5, 7, 11, 13), (1, 3, 27, 2, 4, 26, 28, 24, 30, 23, 25, 29, 31), # 3a0, 3a1 (1, 9, 27, 8, 10, 26, 28, 18, 36, 17, 19, 35, 37), (3, 9, 27, 6, 12, 24, 30, 18, 36, 15, 21, 33, 39) # 3a2, 3a3 ] projections 0     1     2     3     coordinates 0 1 2 3

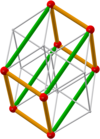
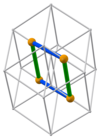
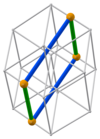
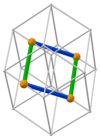
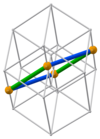
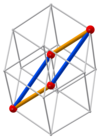
3b 12 cuboids with edge lengths ${\displaystyle 1}$ (orange) and ${\displaystyle {\sqrt {2}}}$ (green)    00

list (2, 3, 4, 4): [ (1, 3, 2, 4, 18, 17, 19, 15, 21, 14, 16, 20, 22), (1, 9, 8, 10, 24, 23, 25, 15, 33, 14, 16, 32, 34), # 3b00, 3b01 (1, 27, 6, 26, 28, 5, 7, 21, 33, 20, 22, 32, 34), (3, 9, 6, 12, 26, 23, 29, 17, 35, 14, 20, 32, 38), # 3b02, 3b03 (3, 27, 8, 24, 30, 5, 11, 19, 35, 16, 22, 32, 38), (9, 27, 2, 18, 36, 7, 11, 25, 29, 16, 20, 34, 38), # 3b04, 3b05 (9, 27, 4, 18, 36, 5, 13, 23, 31, 14, 22, 32, 40), (3, 27, 10, 24, 30, 7, 13, 17, 37, 14, 20, 34, 40), # 3b06, 3b07 (3, 9, 6, 12, 28, 25, 31, 19, 37, 16, 22, 34, 40), (1, 27, 12, 26, 28, 11, 13, 15, 39, 14, 16, 38, 40), # 3b08, 3b09 (1, 9, 8, 10, 30, 29, 31, 21, 39, 20, 22, 38, 40), (1, 3, 2, 4, 36, 35, 37, 33, 39, 32, 34, 38, 40) # 3b10, 3b11 ] 1100, 0011 projections 0     5     11     6     coordinates 0 5 11 6 1010, 0101 projections 1     4     10     7     coordinates 1 4 10 7 0110, 1001 projections 3     2     8     9     coordinates 3 2 8 9

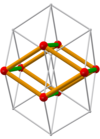
2a 6 squares with edge length ${\displaystyle 1}$ (blue)    00
list (2, 2, 0, 0): [ (1, 3, 2, 4), (1, 9, 8, 10), (3, 9, 6, 12), (1, 27, 26, 28), (3, 27, 24, 30), (9, 27, 18, 36) # 2a0..2a5 ] 1100, 0011 projections 0     5     coordinates 0 5 permutations 0 5 1010, 0101 projections 1     4     coordinates 1 4 permutations 1 4 0110, 1001 projections 2     3     coordinates 2 3 permutations 2 3

2b 24 rectangles with edge lengths ${\displaystyle 1}$ (green) and ${\displaystyle {\sqrt {2}}}$ (blue)    00

list (1, 1, 2, 0): [ (1, 6, 5, 7), (3, 8, 5, 11), (9, 2, 7, 11), (9, 4, 5, 13), (3, 10, 7, 13), (1, 12, 11, 13), # 2b00..2b05 (1, 24, 23, 25), (3, 26, 23, 29), (27, 2, 25, 29), (27, 4, 23, 31), (3, 28, 25, 31), (1, 30, 29, 31), # 2b06..2b11 (1, 18, 17, 19), (9, 26, 17, 35), (27, 8, 19, 35), (27, 10, 17, 37), (9, 28, 19, 37), (1, 36, 35, 37), # 2b12..2b17 (3, 18, 15, 21), (9, 24, 15, 33), (27, 6, 21, 33), (27, 12, 15, 39), (9, 30, 21, 39), (3, 36, 33, 39) # 2b18..2b23 ] 1000 projections 0     6     12     5     11     17     coordinates 0 6 12 5 11 17 0100 projections 1     7     18     4     10     23     coordinates 1 7 18 4 10 23 0010 projections 2     13     19     3     16     22     coordinates 2 13 19 3 16 22 0001 projections 8     14     20     9     15     21     coordinates 8 14 20 9 15 21

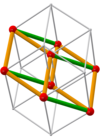
2c 12 squares with edge length ${\displaystyle {\sqrt {2}}}$ (green)    00

list (0, 2, 0, 2): [ (2, 18, 16, 20), (4, 18, 14, 22), (8, 24, 16, 32), (6, 26, 20, 32), (10, 24, 14, 34), (6, 28, 22, 34), # 2c00..2c05 (12, 26, 14, 38), (8, 30, 22, 38), (2, 36, 34, 38), (12, 28, 16, 40), (10, 30, 20, 40), (4, 36, 32, 40) # 2c06..2c11 ] 1100, 0011 projections 0     1     8     11     coordinates 0 1 8 11 1010, 0101 projections 2     4     7     10     coordinates 2 4 7 10 0110, 1001 projections 3     6     5     9     coordinates 3 6 5 9

2d 16 rectangles with edge lengths ${\displaystyle 1}$ (orange) and ${\displaystyle {\sqrt {3}}}$ (blue)

list (1, 0, 1, 2): [ (1, 15, 14, 16), (3, 17, 14, 20), (3, 19, 16, 22), (1, 21, 20, 22), # 2d00..2d03 (9, 23, 14, 32), (27, 5, 22, 32), (9, 25, 16, 34), (27, 7, 20, 34), # 2d04..2d07 (1, 33, 32, 34), (27, 11, 16, 38), (9, 29, 20, 38), (3, 35, 32, 38), # 2d08..2d11 (27, 13, 14, 40), (9, 31, 22, 40), (3, 37, 34, 40), (1, 39, 38, 40) # 2d12..2d15 ] 1000 projections 0 3 8 15 coordinates 0 3 8 15 permutations 0 3 8 15 0100 projections 1 2 11 14 coordinates 1 2 11 14 permutations 1 2 11 14 0010 projections 4 6 10 13 coordinates 4 6 10 13 permutations 4 6 10 13 0001 projections 5 7 9 12 coordinates 5 7 9 12 permutations 5 7 9 12

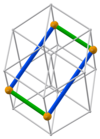
1a 4 line segments with edge length ${\displaystyle 1}$ (between opposite blue points)    00
list (1, 0, 0, 0): [ (1,), (3,), (9,), (27,) # 1a0..1a3 ]
0	1	2	3
permutations

1b 12 line segments with edge length ${\displaystyle {\sqrt {2}}}$ (between opposite green points)    00
list (0, 1, 0, 0): [ (2,), (4,), (8,), (10,), (6,), (12,), (26,), (28,), (24,), (30,), (18,), (36,) # 1b00..1b11 ] 1100, 0011 projections 0     10     1     11     permutations 0 10 1 11 1010, 0101 projections 2     8     3     9     permutations 2 8 3 9 0110, 1001 projections 4     6     5     7     permutations 4 6 5 7

1c 16 line segments with edge length ${\displaystyle {\sqrt {3}}}$ (between opposite yellow points)
list (0, 0, 1, 0): [ (5,), (7,), (11,), (13,), (23,), (25,), (29,), (31,), (17,), (19,), (35,), (37,), (15,), (21,), (33,), (39,) # 1c00..1c15 ] 1110 projections 0 1 2 3 permutations 0 1 2 3 1101 projections 4 5 6 7 permutations 4 5 6 7 1011 projections 8 9 10 11 permutations 8 9 10 11 0111 projections 12 13 14 15 permutations 12 13 14 15

1d 8 line segments with edge length ${\displaystyle {\sqrt {4}}=2}$ (between opposite red points)
list (0, 0, 0, 1): [ (14,), (16,), (20,), (22,), (32,), (34,), (38,), (40,) # 1d0..1d7 ]
0	1	2	3	4	5	6	7
permutations

The origin has the coordinate and number value ${\displaystyle 0}$. So its set of positive face centers is empty. 105 permutations in 5 conjugacy classes leave only the origin unchanged.    00

(0, 0, 0, 0): [ 
    ()
]

The numbers used in the filename refer to the the colexicographic ordering of the positive vertices.
This allows to use the same identifiers for all dimensions. (E.g. cube subspace 2b5 and tesseract subspace 2b05 are the same rectangle with vertices 11 and 13.)
But it is more intuitive to use lexicographic order that takes all face centers into account. (It allows sorting by patterns like 1000.)
The following table shows the lexicographic order of the four kinds of subspaces where the orders differ. (compare code)

These images have been rendered with POV-Ray, and the calculations have been done with Python. The code can be found on GitHub.
The main POV-Ray file is subspaces.pov.
The colored code sections shown above are from the dictionary in e1_store_subspaces.py.