Category:Lattice theory
Jump to navigation
Jump to search
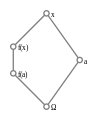
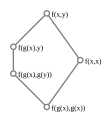
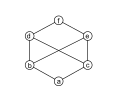
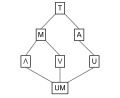
English: In mathematics, a lattice is a partially ordered set (also called a poset) in which any two elements have a unique supremum (the elements' least upper bound; called their join) and an infimum (greatest lower bound; called their meet). Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilattices include lattices, which in turn include Heyting and Boolean algebras. These "lattice-like" structures all admit order-theoretic as well as algebraic descriptions.
branch of mathematics that studies order-theoretic lattices | |||||
| Upload media | |||||
| Instance of | |||||
|---|---|---|---|---|---|
| Part of | |||||
| |||||
Subcategories
This category has the following 8 subcategories, out of 8 total.
Pages in category "Lattice theory"
This category contains only the following page.
Media in category "Lattice theory"
The following 72 files are in this category, out of 72 total.
-
2d modular lattice.svg 288 × 441; 11 KB
-
A De Morgan algebra.png 1,116 × 1,014; 186 KB
-
Abstract interpretation of integers by signs svg.svg 886 × 602; 134 KB
-
Abstract interpretation of integers by signs.pdf 1,475 × 1,002; 20 KB
-
Antimatroid.svg 466 × 327; 5 KB
-
Bands.svg 600 × 630; 3 KB
-
Birkhoff representation theorem.gif 423 × 723; 7 KB
-
Centred hexagon lattice D2.svg 140 × 180; 1 KB
-
Diamond lattice.svg 140 × 180; 867 bytes
-
Diamond-by DrAK.svg 138 × 148; 7 KB
-
Distributive lattice example.svg 270 × 558; 2 KB
-
DistrSemilattice.svg 740 × 670; 3 KB
-
DL Duality.png 353 × 168; 9 KB
-
Dominance order partitions of 6.png 321 × 859; 19 KB
-
Duale Verbaende.svg 270 × 180; 2 KB
-
Dyck lattice D4.svg 1,750 × 2,425; 122 KB
-
ExampleLattice.png 533 × 627; 21 KB
-
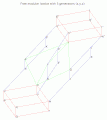
Free distributive lattice with 3 generators (x,y,z).gif 996 × 920; 21 KB
-
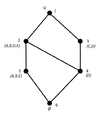
Free modular lattice with 3 generators (x,y,z).gif 807 × 904; 23 KB
-
GaloisEmbeddings Complete Lattices.pdf 1,239 × 1,752, 4 pages; 158 KB
-
Generalizations of abc.gif 516 × 536; 6 KB
-
Hasse Diagram of Subgroup Lattice of D4.png 1,607 × 767; 43 KB
-
Hexagon lattice.svg 140 × 180; 876 bytes
-
KeinVerband.svg 80 × 80; 960 bytes
-
Lattice 2.jpg 153 × 127; 15 KB
-
Lattice M4.svg 190 × 180; 952 bytes
-
Lexicographic order on pairs of natural numbers.svg 1,600 × 1,200; 18 KB
-
M 3 mit Beschriftung.svg 120 × 120; 946 bytes
-
M3 1xyz0.svg 140 × 180; 1 KB
-
M3 abcde.svg 140 × 180; 1 KB
-
M3 Lattice.png 292 × 213; 5 KB
-
M3 linear terms.svg 140 × 180; 1 KB
-
Metric lattice cube135.svg 170 × 170; 8 KB
-
Monotonic but nonhomomorphic map between lattices.gif 714 × 400; 4 KB
-
N 5 mit Beschriftung.svg 180 × 180; 847 bytes
-
N-Quadrat, gedreht.svg 260 × 200; 5 KB
-
N5 1bax0.svg 140 × 180; 951 bytes
-
N5 1xyz0.svg 140 × 180; 951 bytes
-
N5 abcde.svg 140 × 180; 951 bytes
-
N5 Lattice.png 292 × 213; 5 KB
-
N5 linear terms.svg 140 × 180; 958 bytes
-
N5 terms.svg 160 × 180; 991 bytes
-
Nat num x 2+.svg 120 × 130; 3 KB
-
Nat num.svg 120 × 120; 1 KB
-
NoLatticeDiagram.svg 488 × 413; 13 KB
-
Non-dstrbtive lattices-warning.png 434 × 202; 7 KB
-
Non-dstrbtive lattices-warning.svg 348 × 139; 14 KB
-
Non-dstrbtive lattices.png 454 × 202; 7 KB
-
Non-dstrbtive lattices.svg 346 × 139; 26 KB
-
PairsOfSquaresLattice.gif 751 × 785; 21 KB
-
Pairwise unifiable terms.gif 873 × 456; 7 KB
-
Post lattice with constants.svg 180 × 190; 2 KB
-
Post-lattice-constants.svg 512 × 416; 7 KB
-
Post-lattice.png 975 × 1,080; 130 KB
-
Post-lattice.svg 650 × 720; 17 KB
-
Pow3nonlattice.svg 429 × 415; 6 KB
-
Rehasse.png 78 × 141; 1 KB
-
Ret1.png 295 × 195; 5 KB
-
Ret2.png 194 × 83; 2 KB
-
RetL.png 70 × 120; 2 KB
-
RetL1.png 70 × 70; 2 KB
-
RetM.png 89 × 106; 2 KB
-
RetN5.png 65 × 98; 4 KB
-
Retndistr.png 163 × 127; 3 KB
-
Smallest nonmodular lattice 1.svg 140 × 180; 788 bytes
-
Smallest nonmodular lattice 2.svg 200 × 160; 938 bytes
-
Strict product order on pairs of natural numbers.svg 850 × 900; 51 KB
-
Tevetlattice.jpg 1,053 × 838; 329 KB
-
TwRepr-1.svg 735 × 406; 64 KB
-
TwRepr-2.svg 735 × 406; 39 KB
-
Verband monotonesBild.png 277 × 172; 3 KB
-
Young5.svg 792 × 585; 7 KB