File:Paritition of dynamic plane of quadratic polynomial for 1 4.svg
From Wikimedia Commons, the free media repository
Jump to navigation
Jump to search

Size of this PNG preview of this SVG file: 600 × 600 pixels. Other resolutions: 240 × 240 pixels | 480 × 480 pixels | 768 × 768 pixels | 1,024 × 1,024 pixels | 2,048 × 2,048 pixels | 1,000 × 1,000 pixels.
Original file (SVG file, nominally 1,000 × 1,000 pixels, file size: 430 KB)
File information
Structured data
Captions
Captions
Paritition of dynamic plane of quadratic polynomial for 1/9
Summary
[edit]| DescriptionParitition of dynamic plane of quadratic polynomial for 1 4.svg |
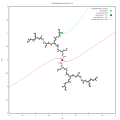
English: Paritition of dynamic plane of critically preperiodic quadratic polynomial for external ray t = 1/4 landing at the critical value z= c = -0.228155493653962 +1.115142508039937*i period = 0. Preperiod = 2 period = 1 |
| Date | |
| Source | Own work |
| Author | Adam majewski |
| Other versions |
|
| SVG development InfoField | This plot uses embedded text that can be easily translated using a text editor. |
Licensing
[edit]I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Maxima CAS src code
[edit] /*
batch file for Maxima CAS
maxima
batch("k.mac");
------------ program Mandel by Wolf Jung -------------------------
The angle 3/30 or 0p0011
has preperiod = 1 and period = 4.
The corresponding parameter ray is landing
at a Misiurewicz point of preperiod 1 and
period dividing 4.
Do you want to draw the ray and to shift c
to the landing point?
-------------------
*/
kill(all);
remvalue(all);
ratprint:false; /* It doesn't change the computing, just the warnings. */
display2d:false;
/* --------------------------definitions of functions ------------------------------*/
f(z,c):=z*z+c; /* Complex quadratic map */
finverseplus(z,c):=float(rectform(sqrt(z-c)))$
finverseminus(z,c):=float(rectform(-sqrt(z-c)))$
/* */
fn(p, z, c) :=
if p=0 then z
elseif p=1 then f(z,c)
else f(fn(p-1, z, c),c)$
/*Standard polynomial F_p \, which roots are periodic z-points of period p and its divisors */
F(p, z, c) := fn(p, z, c) - z $
/* Function for computing reduced polynomial G_p\, which roots are periodic z-points of period p without its divisors*/
G[p,z,c]:=
block(
[f:divisors(p),
t:1], /* t is temporary variable = product of Gn for (divisors of p) other than p */
f:delete(p,f), /* delete p from list of divisors */
if p=1
then return(F(p,z,c)),
for i in f do
t:t*G[i,z,c],
g: F(p,z,c)/t,
return(ratsimp(g))
)$
GiveRoots(g):=
block(
[cc],
cc:bfallroots(expand(%i*g)=0),
cc:map(rhs,cc),/* remove string "c=" */
cc:map('float,cc),
return(cc)
)$
/* Gives points of backward orbit of z=repellor
problem for 1/10
*/
GiveBackwardOrbit(c,repellor,zxMin,zxMax,zyMin,zyMax,iXmax,iYmax, hit_limit):=
block(
hit_limit:10, /* proportional to number of details and time of drawing */
PixelWidth:(zxMax-zxMin)/iXmax,
PixelHeight:(zyMax-zyMin)/iYmax,
/* 2D array of hits pixels . Hit > 0 means that point was in orbit */
array(Hits,fixnum,iXmax,iYmax), /* no hits for beginning */
/* choose repeller z=repellor as a starting point */
stack:[repellor], /*save repellor in stack */
/* save first point to list of pixels */
x_y:[repellor],
/* reversed iteration of repellor */
loop,
/* pop = take one point from the stack */
z:last(stack),
stack:delete(z,stack),
/*inverse iteration - first preimage (root) */
z:finverseplus(z,c),
/* translate from world to screen coordinate */
iX:fix((realpart(z)-zxMin)/PixelWidth),
iY:fix((imagpart(z)-zyMin)/PixelHeight),
hit:Hits[iX,iY],
if hit<hit_limit
then
(
Hits[iX,iY]:hit+1,
stack:endcons(z,stack), /* push = add z at the end of list stack */
if hit=0 then x_y:endcons( z,x_y)
),
/*inverse iteration - second preimage (root) */
z:-z,
/* translate from world to screen coordinate, coversion to integer */
iX:fix((realpart(z)-zxMin)/PixelWidth),
iY:fix((imagpart(z)-zyMin)/PixelHeight),
hit:Hits[iX,iY],
if hit<hit_limit
then
(
Hits[iX,iY]:hit+1,
stack:endcons(z,stack), /* push = add z at the end of list stack to continue iteration */
if hit=0 then x_y:endcons( z,x_y)
),
if is(not emptyp(stack)) then go(loop),
return(x_y) /* list of pixels in the form [z1,z2] */
)$
/*-----------------------------------*/
Psi_n(r,t,z_last, Max_R):=
/* */
block(
[iMax:200,
iMax2:0],
/* ----- forward iteration of 2 points : z_last and w --------------*/
array(forward,iMax-1), /* forward orbit of z_last for comparison */
forward[0]:z_last,
i:0,
while cabs(forward[i])<Max_R and i< ( iMax-2) do
(
/* forward iteration of z in fc plane & save it to forward array */
forward[i+1]:forward[i]*forward[i] + c, /* z*z+c */
/* forward iteration of w in f0 plane : w(n+1):=wn^2 */
r:r*2, /* square radius = R^2=2^(2*r) because R=2^r */
t:mod(2*t,1),
/* */
iMax2:iMax2+1,
i:i+1
),
/* compute last w point ; it is equal to z-point */
R:2^r,
/* w:R*exp(2*%pi*%i*t), z:w, */
array(backward,iMax-1),
backward[iMax2]:float(rectform(ev(R*exp(2*%pi*%i*t)))), /* use last w as a starting point for backward iteration to new z */
/* ----- backward iteration point z=w in fc plane --------------*/
for i:iMax2 step -1 thru 1 do
(
temp:float(rectform(sqrt(backward[i]-c))), /* sqrt(z-c) */
scalar_product:realpart(temp)*realpart(forward[i-1])+imagpart(temp)*imagpart(forward[i-1]),
if (0>scalar_product) then temp:-temp, /* choose preimage */
backward[i-1]:temp
),
return(backward[0])
)$
/* problems for c= -2 and t = 1/2 */
GiveRay(t,c):=
block(
[r],
/* range for drawing R=2^r ; as r tends to 0 R tends to 1 */
rMin:1E-10, /* 1E-4; rMin > 0 ; if rMin=0 then program has infinity loop !!!!! */
rMax:3,
dz : 100, /* dz : cabs ( z - last_z) ; if dz is to small then loop is not ending */
MachineEpsilonDouble: 1E-16,
caution:0.9330329915368074, /* r:r*caution ; it gives smaller r */
/* upper limit for iteration */
R_max:300,
/* */
zz:[], /* array for z points of ray in fc plane */
/* some w-points of external ray in f0 plane */
r:rMax,
while 2^r<R_max do r:2*r, /* find point w on ray near infinity (R>=R_max) in f0 plane */
R:2^r,
w:float(rectform(ev(R*exp(2*%pi*%i*t)))),
z:w, /* near infinity z=w */
zz:cons(z,zz),
unless (r<rMin or dz < MachineEpsilonDouble) do
( /* new smaller R */
r:r*caution,
R:2^r,
/* */
w:float(rectform(ev(R*exp(2*%pi*%i*t)))),
/* */
last_z:z,
z:Psi_n(r,t,last_z,R_max), /* z=Psi_n(w) */
dz : cabs ( z - last_z),
zz:cons(z,zz)
),
return(zz)
)$
/*
converts complex number z = x*y*%i
to the list in a draw format:
[x,y]
*/
d(z):=[float(realpart(z)), float(imagpart(z))]$
ToPoints(myList):= points(map(d,myList))$
/* give Draw List from one point*/
ToPoint(z):=points([d(z)])$
/* compile(all)$ */
/* ----------------------- main ----------------------------------------------------*/
start:elapsed_run_time ();
HitLimit:15$ /* proportional to number of details and time of drawing */
/* external angle in turns */
/* resolution is proportional to number of details and time of drawing */
iX_max:1000$
iY_max:1000$
/* define z-plane ( dynamical ) */
ZxMin:-2.0$
ZxMax:2.0$
ZyMin:-2.0$
ZyMax:2.0$
t:1/4;
/* give c a value */
c: -0.228155493653962 +1.115142508039937*%i $ /* one can compute it from t */
/* compute fixed points */
Beta:float(rectform((1+sqrt(1-4*c))/2)); /* compute repelling fixed point beta */
alfa:float(rectform((1-sqrt(1-4*c))/2)); /* other fixed point */
/* compute backward orbit of repelling fixed point*/
xy: GiveBackwardOrbit(c,Beta,ZxMin,ZxMax,ZyMin,ZyMax,iX_max,iY_max, HitLimit)$
/* compute ray points & save to zz list */
eRay : GiveRay(t,c)$
eRayT:GiveRay(t/2,c)$
eRayTp:GiveRay((t+1)/2,c)$
/* time of computations */
time:fix(elapsed_run_time ()-start);
/* draw it using draw package by */
load(draw)$
path:"/"$ /* if empty then file is in a home dir */
/* if graphic file is empty (= 0 bytes) then run draw2d command again */
draw2d(
terminal = 'svg,
file_name = sconcat(path,"a",string(HitLimit)),
user_preamble="set size square;set key top right",
title= concat("Dynamical plane for fc(z)=z*z+",string(c)),
dimensions = [iX_max, iY_max],
yrange = [ZyMin,ZyMax],
xrange = [ZxMin,ZyMax],
xlabel = "Z.re ",
ylabel = "Z.im",
point_type = filled_circle,
points_joined =true,
point_size = 0.2,
color = red,
points_joined =false,
color = black,
key = "backward orbit of z=beta",
points(map(realpart,xy),map(imagpart,xy)),
points_joined =false,
color = green,
point_size = 1.4,
key = "critical value",
ToPoint(c),
key = sconcat("external ray t=",string(t)),
color = green,
points_joined =true,
point_size = 0.2,
ToPoints(eRay),
points_joined = false,
color = black,
point_size = 1.4,
key = "critical point z = 0.0",
ToPoint(0.0),
points_joined =true,
point_size = 0.2,
color = red,
key = sconcat("external ray t/2 = ", string(t/2)),
ToPoints(eRayT),
key = sconcat("external ray (t+1)/2 =",string((t+1)/2)),
color = magenta,
ToPoints(eRayTp)
)$
Text output
[edit](%i17) start:elapsed_run_time() (%o17) 0.07 (%i18) HitLimit:15 (%i19) iX_max:1000 (%i20) iY_max:1000 (%i21) ZxMin:-2.0 (%i22) ZxMax:2.0 (%i23) ZyMin:-2.0 (%i24) ZyMax:2.0 (%i25) t:1/4 (%o25) 1/4 (%i26) c:(-0.228155493653962)+1.115142508039937*%i (%i27) Beta:float(rectform((1+sqrt(1-4*c))/2)) (%o27) 1.41964337760708-0.6062907292071991*%i (%i28) alfa:float(rectform((1-sqrt(1-4*c))/2)) (%o28) 0.6062907292071991*%i-0.4196433776070805
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:00, 14 July 2019 |  | 1,000 × 1,000 (430 KB) | Soul windsurfer (talk | contribs) | User created page with UploadWizard |
You cannot overwrite this file.
File usage on Commons
The following 3 pages use this file:
File usage on other wikis
The following other wikis use this file:
- Usage on el.wikipedia.org
- Usage on en.wikipedia.org
- Usage on en.wikibooks.org
- Fractals/Iterations in the complex plane/def cqp
- Fractals/Iterations in the complex plane/jlamination
- Fractals/mandel
- Fractals/Iterations in the complex plane/MandelbrotSetExterior/ParameterExternalRay
- Fractals/Iterations in the complex plane/misiurewicz
- Fractals/Iterations in the complex plane/dynamic external rays
Metadata
This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.
| Short title | Gnuplot |
|---|---|
| Image title | Produced by GNUPLOT 5.3 patchlevel 0 |
| Width | 1000 |
| Height | 1000 |