File:Line integral of scalar field.gif
Line_integral_of_scalar_field.gif (400 × 300 pixels, file size: 580 KB, MIME type: image/gif, looped, 61 frames, 39 s)
Captions
Captions
Summary
[edit]| DescriptionLine integral of scalar field.gif |
English: Line integral of a scalar field, f. The area under the curve C, traced on the surface defined by z = f(x,y), is the value of the integral. See full description.
فارسی: انتگرال خطی یک میدان اسکالر f. مقدار انتگرال مساحت زیر منحنی C تعریف شده توسط سطح (z = f(x,y است.
Français : L′intégrale curviligne d′un champ scalaire, f. L′aire sous la courbe C, tracée sur la surface définie par z = f(x,y), est la valeur de l'intégrale.
Italiano: Integrale di linea di un campo scalare, f. Il valore dell'integrale è pari all'area sotto la curva C, tracciata sulla superficie definita da z = f(x,y).
Русский: Иллюстрация криволинейного интеграла первого рода на скалярном поле. |
|||
| Date | ||||
| Source | Own work | |||
| Author | Lucas Vieira | |||
| Permission (Reusing this file) |
|
|||
| Other versions |
Assessment
[edit]
|

|
This image was selected as picture of the day on Wikimedia Commons for 11 April 2013. It was captioned as follows: English: Line integral of a scalar field, f. The area under the curve C, traced on the surface defined by z = f(x,y), is the value of the integral. Other languages:
Deutsch: Illustration eines Kurvenintegrals erster Art über ein Skalarfeld, f. Das Gebiet unter der Kurve C, abgetragen auf die Oberfläche definiert von z = f(x,y), ist der Wert des Integrals. English: Line integral of a scalar field, f. The area under the curve C, traced on the surface defined by z = f(x,y), is the value of the integral. Français : L′intégrale curviligne d′un champ scalaire, f. L′aire sous la courbe C, tracée sur la surface définie par z = f(x,y), est la valeur de l'intégrale. Italiano: Integrale di linea di un campo scalare, f. Il valore dell'integrale è pari all'area sotto la curva C, tracciata sulla superficie definita da z = f(x,y). Magyar: Az f skalártér vonal menti integrálja. Az integrál értéke a z=f(x,y) függvénnyel definiált C görbe alatti terület. Nederlands: Lijnintegraal van een scalair veld, f. Het gebied onder de curve C, getraceerd op het vlak gedefinieerd door z = f(x,y), is de waarde van de integraal. |
Full description (English)
[edit]A scalar field has a value associated to each point in space. Examples of scalar fields are height, temperature or pressure maps. In a two-dimensional field, the value at each point can be thought of as a height of a surface embedded in three dimensions. The line integral of a curve along this scalar field is equivalent to the area under a curve traced over the surface defined by the field.
In this animation, all these processes are represented step-by-step, directly linking the concept of the line integral over a scalar field to the representation of integrals familiar to students, as the area under a simpler curve. A breakdown of the steps:
- The color-coded scalar field f and a curve C are shown. The curve C starts at a and ends at b
- The field is rotated in 3D to illustrate how the scalar field describes a surface. The curve C, in blue, is now shown along this surface. This shows how at each point in the curve, a scalar value (the height) can be associated.
- The curve is projected onto the plane XY (in gray), giving us the red curve, which is exactly the curve C as seen from above in the beginning. This is red curve is the curve in which the line integral is performed. The distances from the projected curve (red) to the curve along the surface (blue) describes a "curtain" surface (in blue).
- The graph is rotated to face the curve from a better angle
- The projected curve is rectified (made straight), and the same transformation follows on the blue curve, along the surface. This shows how the line integral is applied to the arc length of the given curve
- The graph is rotated so we view the blue surface defined by both curves face on
- This final view illustrates the line integral as the familiar integral of a function, whose value is the "signed area" between the X axis (the red curve, now a straight line) and the blue curve (which gives the value of the scalar field at each point). Thus, we conclude that the two integrals are the same, illustrating the concept of a line integral on a scalar field in an intuitive way.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 16:43, 14 August 2012 | 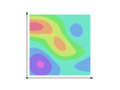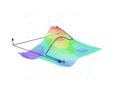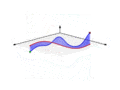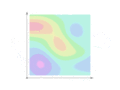 | 400 × 300 (580 KB) | LucasVB (talk | contribs) | Unoptimized. Sticking with local palettes for better color resolution per frame. Added bands of color to the field instead of a smooth gradient. Overall, it should look sharper, though the file will be bigger. Worth it, I say! |
| 12:24, 25 July 2012 | 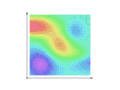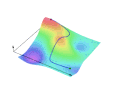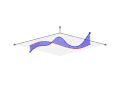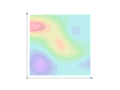 | 400 × 300 (328 KB) | LucasVB (talk | contribs) | Alternative illustration of the "straightening" of the curve. It should convey the concept better than the previous one, which may be interpreted as a mere projection. Also, changed to pattern dithering. Seems to look better, and file is smaller even t... | |
| 16:59, 24 July 2012 |  | 400 × 300 (337 KB) | LucasVB (talk | contribs) | {{Information |Description= |Source={{own}} |Date=2012-07-24 |Author= Kieff |Permission={{PD-self}} |other_versions= }} |
You cannot overwrite this file.
File usage on Commons
The following 58 pages use this file:
- User:LucasVB/Profile
- User:Ö/Best/2012
- User talk:LucasVB/Archive0
- Commons:Bu proje sayfasının diğer dil sürümleri
- Commons:Conhece os nossos ilustradores
- Commons:Conoce a nuestros ilustradores
- Commons:Descobrètz nòstres illustrators
- Commons:Découvrez nos illustrateurs
- Commons:Featured picture candidates/File:Line integral of scalar field.gif
- Commons:Featured picture candidates/Log/August 2012
- Commons:Featured pictures/Animated
- Commons:Featured pictures/chronological/2012-B
- Commons:Meet our illustrators
- Commons:Meet our illustrators/People
- Commons:Picture of the Year/2012/Finalists
- Commons:Picture of the Year/2012/Finalists/Line integral of scalar field.gif
- Commons:Picture of the Year/2012/Galleries/2012-B
- Commons:Picture of the Year/2012/Galleries/ALL
- Commons:Picture of the Year/2012/Galleries/AUG
- Commons:Picture of the Year/2012/Galleries/Index/12
- Commons:Picture of the Year/2012/Galleries/Videos
- Commons:Picture of the Year/2012/R1/Line integral of scalar field.gif
- Commons:Picture of the Year/2012/Results/R1/ALL
- Commons:Picture of the Year/2012/Results/R1/ALL/gallery
- Commons:Picture of the Year/2012/Results/R1/ALL/thumbnailtable
- Commons:Picture of the Year/2012/Results/R1/Category
- Commons:Picture of the Year/2012/Results/R1/Checking
- Commons:Picture of the Year/2012/Results/R1/Finalists
- Commons:Picture of the Year/2012/Results/R1/Videos
- Commons:Picture of the Year/2012/Results/R2
- Commons:Picture of the Year/2012/Results/R2/thumbnailtable
- Commons:Picture of the Year/2012/Translations
- Commons:Picture of the Year/2012/Translations/table/Captions
- Commons:Poznaj naszych grafików
- Commons:Scopri i nostri illustratori
- Commons:Scummigghia ê nostri llustratura
- Commons:Unsere Illustratoren stellen sich vor
- Commons:Unseri Illustratore stelle sich vor
- Commons:Upoznajte naše ilustratore
- Commons:Çizerlerimizle tanışın
- Commons:Запознајте ги нашите илустратори
- Commons:Знайомтесь з нашими ілюстраторами
- Commons:Знакомьтесь с нашими иллюстраторами
- Commons:قابل رسامينا
- Commons:私達のイラストレータをご紹介します
- Commons:结识我们的插图师
- Commons:우리들의 삽화가를 만나보세요
- Template:Potd/2013-04
- Template:Potd/2013-04-11
- Template:Potd/2013-04-11 (de)
- Template:Potd/2013-04-11 (en)
- Template:Potd/2013-04-11 (fr)
- Template:Potd/2013-04-11 (hu)
- Template:Potd/2013-04-11 (it)
- Template:Potd/2013-04-11 (ko)
- Template:Potd/2013-04-11 (nl)
- Template:Potd/2013-04-11 (zh-hans)
- Template:Potd/2013-04 (zh-hans)
File usage on other wikis
The following other wikis use this file:
- Usage on ar.wikipedia.org
- Usage on be-tarask.wikipedia.org
- Usage on bg.wikipedia.org
- Usage on bn.wikipedia.org
- Usage on ca.wikipedia.org
- Usage on ckb.wikipedia.org
- Usage on crh.wikipedia.org
- Usage on cs.wikipedia.org
- Usage on cv.wikipedia.org
- Usage on da.wikipedia.org
- Usage on de.wikipedia.org
- Usage on de.wikiversity.org
- Usage on el.wikipedia.org
- Usage on en.wikipedia.org
- Talk:Line integral
- User talk:LucasVB
- User:LucasVB/Gallery
- Portal:Mathematics/Featured picture archive
- Line integral
- Wikipedia:WikiProject Mathematics/Recognized content
- Wikipedia:Featured pictures/Sciences/Mathematics
- Wikipedia:Featured pictures thumbs/31
- Wikipedia:Featured picture candidates/August-2012
- Wikipedia:Featured picture candidates/Line integral of scalar field
- Wikipedia:Wikipedia Signpost/2012-09-03/Featured content
- Wikipedia:Wikipedia Signpost/Single/2012-09-03
- User:Mediation4u/todo/finance
- User:Montanamichael5/Media/Images/POTY/2012/Round 2
- User:Montanamichael5/Media/Images/POTY
- Wikipedia:Picture of the day/November 2013
- Template:POTD/2013-11-12
- Portal:Mathematics/Selected picture
- Wikipedia:Main Page history/2013 November 12
- Portal:Mathematics/Featured picture/2013 11
- Portal:Mathematics/Selected picture/7
- User:VGrigas (WMF)/Quality Media
- User:Vector Mobile
- Portal:Mathematics/Recognized content
- Usage on en.wikibooks.org
- Usage on es.wikipedia.org
View more global usage of this file.
- Self-published work
- PD-self
- Pictures of the Year (finalist)
- Pictures of the Year (candidate)
- Pictures of the Year (2012)
- Featured pictures on Wikimedia Commons
- Featured pictures on Wikipedia, English
- Featured pictures on Wikipedia, Persian
- Pictures of the day (2013)
- Featured animations
- Posted to Wikimedia Foundation Pinterest
- Animated GIF files
- Featured pictures in the public domain

