File:FS RV dia.png

Original file (687 × 601 pixels, file size: 20 KB, MIME type: image/png)
Captions
Captions
Contents
Summary
[edit]| DescriptionFS RV dia.png |
English: Largest quarter circle in a rectangular isosceles triangle
Deutsch: Größer Viertelkreis in einem gleichschenkligen rechtwinkligen Dreieck |
| Date | |
| Source | Own work |
| Author | Hans G. Oberlack |
Shows the largest quarter circle within a right isosceles triangle.

Elements
[edit]Base is the right isosceles triangle of side length 

Inscribed is the largest possible quarter circle with radius 
General case
[edit]
Segments in the general case
[edit]0) The side length of the base right triangle
1) Radius of the quarter circle 
Perimeters in the general case
[edit]0) Perimeter of base triangle 
1) Perimeter of the quarter circle 
Areas in the general case
[edit]0) Area of the base triangle
1) Area of the inscribed circle 
Centroids in the general case
[edit]Centroid positions are measured from the centroid point of the base shape
0) Centroid positions of the base triangle:
1) Centroid positions of the inscribed quarter circle: 
Normalised case
[edit]
In the normalised case the area of the base is set to 1.
Segments in the normalised case
[edit]0) Side length of the base triangle
1) Radius of the inscribed quarter circle
Perimeters in the normalised case
[edit]0) Perimeter of base triangle 
1) Perimeter of the inscribed quarter circle
S) Sum of perimeters
Areas in the normalised case
[edit]0) Area of the base triangle
1) Area of the inscribed quarter circle
Centroids in the normalised case
[edit]Centroid positions are measured from the centroid point of the base shape.
0) Centroid positions of the base triangle:
1) Centroid positions of the inscribed circle:
Distances of centroids
[edit]The distance between the centroid of the base element and the centroid of the circle is:
Identifying number
[edit]Apart of the base element there is only one shape allocated. Therefore the integer part of the identifying number is 1.
The decimal part of the identifying number is the decimal part of the sum of the perimeters and the distances of the centroids in the normalised case.
So the identifying number is: 
Calculations
[edit]Calculation 1
[edit]Because FS_R is a right isosceles triangle the following equations hold:
(1)
(2)
(3)
(4)
Since 



(5)

Calculation 2
[edit]Perimeter of the quarter circle:
Calculation 3
[edit]Area of the inscribed quarter circle:
Calculation 4
[edit]Centroid of the inscribed circle measured from the centroid of the base triangle:
-->
Licensing
[edit]- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 19:09, 12 March 2022 |  | 687 × 601 (20 KB) | Hans G. Oberlack (talk | contribs) | upload corrected |
| 17:55, 12 March 2022 | 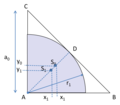 | 687 × 601 (20 KB) | Hans G. Oberlack (talk | contribs) | Uploaded own work with UploadWizard |
You cannot overwrite this file.
File usage on Commons
The following 2 pages use this file:
Metadata
This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.
| Horizontal resolution | 59.06 dpc |
|---|---|
| Vertical resolution | 59.06 dpc |
| Software used |








































