File:Cx linéaire prismes rectangulaires en régime de Stokes d'après Sunada et coll.png
Original file (1,181 × 579 pixels, file size: 71 KB, MIME type: image/png)
Captions
Captions
Summary
[edit]| DescriptionCx linéaire prismes rectangulaires en régime de Stokes d'après Sunada et coll.png |
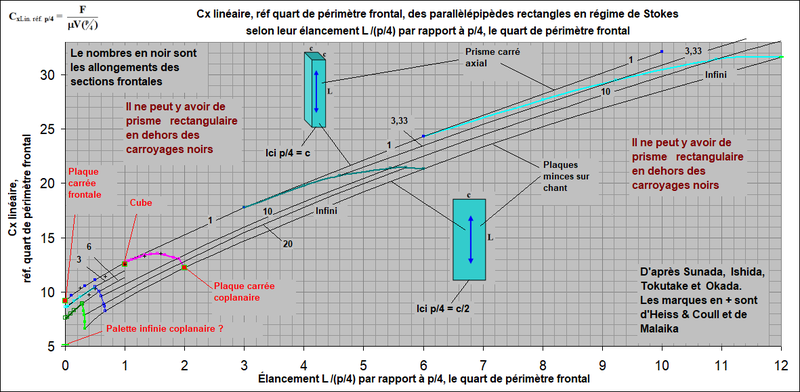
Français : Cx linéaire de Lamb, c-à-d Traînée / (µVL), L étant une longueur caractéristique (ici le quart de périmètre de la section frontale), des prismes rectangulaires, d'après Sunada, Ishida, Tokutake et Okada.
English: Linear Cd of Lamb, i.e. Drag / (µVL), L being a characteristic length (here the quarter of the frontal perimeter), of rectangular prisms, after Sunada, Ishida, Tokutake and Okada. |
| Date | |
| Source | Own work |
| Author | Bernard de Go Mars |
Licensing
[edit]- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
| Annotations InfoField | This image is annotated: View the annotations at Commons |
Pour dessiner ces courbes, nous avons exploité principalement :
FLUID DYNAMIC FORCE ACTING ON A RECTANGULAR SOLID IN A STOKES FLOW, S. Sunada; R. Ishida; H. Tokutake : https://arc.aiaa.org/doi/abs/10.2514/1.42386
et: FLUID DYNAMIC FORCES ACTING ON RECTANGULAR PLATE WITH HOLE IN STOKES FLOW, S.Sunada, H. Tokutake, S. Okada : https://www.jstage.jst.go.jp/article/tjsass/53/181/53_181_231/_pdf
Il ne peut exister de prisme rectangulaire présentant un Cx linéaire (défini comme précisé) au dessus de la ligne noire marquée "1" et en-dessous de la ligne noire marquée "Infini".
Le Cx linéaire de la palette infinie se déplaçant parallèlement à sa plus grande dimension (l'autre dimension étant faible) a été déterminé par des réflexions hyperboliques à partir des valeurs de Sunada et coll, malheureusement pour des élancements trop faibles.
Les nombres en noir représentent l'allongement c/c' de la section frontale, c étant le grand côté de cette section et c' le petit côté. Pour les prismes de section carrée se déplaçant axialement, cet allongement est donc 1. Pour les plaques minces se déplaçant sur chant, cet allongement devient infini (puisque c'= 0)...
Les courbes en couleur représentent le Cx linéaire (réf. p/4) des prismes de Sunada et coll. Par exemple, cette courbe bleu clair représente le Cx linéaire du prisme initialement de section carrée (élancement classique et p/4 : 6) se déplaçant axialement ; cependant le côté c' de la section frontale s'amenuise de gauche à droite pour devenir nul (l'allongement de la section frontale passant alors de 1 à l'Infini).
Les valeurs expérimentales d'Heiss & Coull et de Malaika (marques en +) vérifient assez fidèlement l'étagement des courbes noires marquées 1, 3, 6.
La longueur de référence choisie ici est le quart du périmètre de la section frontale, de façon que, pour le prisme de section carrée en déplacements axiaux, ladite longueur de référence redevient le côté c de la section carrée.
Pour les plaques minces se déplaçant sur chant, c'= 0 et le quart de périmètre devient c/2.
La longueur de référence choisie ici est le quart du périmètre de la section frontale, de façon que, pour le prisme de section carrée en déplacements axiaux, ladite longueur de référence redevient le côté c de la section carrée. Il faut noter que cette longueur de référence est également la moyenne des côtés c et c' des surfaces frontales.
Les courbes en couleur représentent le Cx linéaire (réf. p/4) des prismes de Sunada et coll. Par exemple, cette courbe bleu clair représente le Cx linéaire du prisme initialement de section carrée (élancement classique et p/4 : 6) se déplaçant axialement ; cependant le côté c' de la section frontale s'amenuise de gauche à droite pour devenir nul (l'allongement de la section frontale passant alors de 1 à l'Infini).
Les nombres en noir représentent l'allongement c/c' de la section frontale, c étant le grand côté de cette section et c' le petit côté. Pour les prismes de section carrée se déplaçant axialement, cet allongement est donc 1. Pour les plaques minces se déplaçant sur chant, cet allongement devient infini (puisque c'= 0)...
Pour les plaques minces se déplaçant sur chant, c'= 0 et le quart de périmètre devient c/2.
Il ne peut exister de prisme rectangulaire présentant un Cx linéaire (défini comme précisé) au dessus de la ligne noire marquée "1" et en-dessous de la ligne noire marquée "Infini".
Les valeurs expérimentales d'Heiss & Coull et de Malaika vérifient assez fidèlement l'étagement du carroyage noir.
Le Cx linéaire de la palette infinie se déplaçant parallèlement à sa plus grande dimension (l'autre dimension étant faible) a été déterminé par des réflexions hyperboliques à partir des valeurs de Sunada et coll.
Pour dessiner ces courbes, nous avons exploité principalement :
FLUID DYNAMIC FORCE ACTING ON A RECTANGULAR SOLID IN A STOKES FLOW, S. Sunada; R. Ishida; H. Tokutake : https://arc.aiaa.org/doi/abs/10.2514/1.42386
et: FLUID DYNAMIC FORCES ACTING ON RECTANGULAR PLATE WITH HOLE IN STOKES FLOW, S.Sunada, H. Tokutake, S. Okada : https://www.jstage.jst.go.jp/article/tjsass/53/181/53_181_231/_pdf
Comme on le voit, l'écart entre la courbe noire supérieure (marquée 1) et la courbe noire inférieure (marquée Infini) est assez proche de 4 à 3 (en allant vers la droite). Comme les surfaces frontales (avant et arrière) des prismes de même longueur ET à la même abscisse s'amenuise pour atteindre 0 (à la courbe noire marquée Infini), on peut avoir l'idée que cette diminution de l'ordonnée (du Cx linéaire) est liée à la diminution des deux surfaces frontales et donc du Cx de pression s'exerçant sur ces surfaces frontales. C'est vrai simplement en ordre de grandeur ainsi que le montre la courbe en tiretés gros vert, ce qui justifie le recours par Bowen et Masliyah à un prisme à base carrée équivalent (de même surface latérale ou même périmètre).
Cette courbe en tiretés gros vert représente le Cx de pression des faces frontales (avant et arrière) du prisme à base carré en décantation axiale (courbe noire marquée 1) selon son élancement p/4. On note que cette composante de pression est assez proche, en ordre de grandeur, de l'écart, à la même abscisse, entre les courbes noires marquées 1 et Infini. Tout se passe donc à peu près comme si la disparition des surfaces frontales (à mesure qu'on descend de la courbe noire marquée 1 à la courbe noire marquée Infini) amenuisait jusqu'à zéro le Cx de pression ressenti par le prisme sur ses faces frontales. Ceci justifie quelque peu le recours, par Bowen et Masliyah, à un prisme à base carrée équivalent (de même périmètre frontal).
Que représente cet élancement quart-périmètre ?
Cet élancement quart-périmètre (ou élancement p/4) représente l’élancement frontal L /[(2c+2c')/4] d’un prisme rectangulaire par rapport à la moyenne des côtés c et c' de sa section frontale. Comme on le voit, c’est aussi le quotient de sa longueur L (prise parallèlement au déplacement) par la moyenne (c+c')/2 = p/4 des côtés de sa section frontale (section faisant face au mouvement). Cet élancement p/4 a donc une signification physique assez banale et apparaît comme un moyen pratique de calculer l’élancement d’un corps (nombre qui se doit d'être adimensionnel). Pour le prisme à base carrée, cet élancement p/4 est l’élancement L/c classique. Cette définition reste valable pour un corps quelconque, non prismatique, par exemple, le périmètre étant dans ce cas celui de la section frontale faisant face au mouvement comme pratiqué aux hauts Reynolds).
Comme on le voit, l'écart en ordonnées entre la courbe noire supérieure (marquée 1) et la courbe noire inférieure (marquée Infini) est assez proche de 4 à 3 (en allant vers la droite). Il faut réaliser que, sur une même verticale, les corps de même longueur L présentent le même quart de périmètre p/4, donc le même périmètre.
Que représente cet élancement quart-périmètre ?
Le libellé de cet élancement quart-périmètre (ou élancement p/4) est L /[(2c+2c')/4]. Comme on le voit, c’est aussi le quotient de sa longueur L (prise parallèlement au déplacement) par la moyenne (c+c')/2 = p/4 des côtés de sa section frontale (section faisant face au mouvement). Cet élancement p/4 a donc une signification physique assez banale et apparaît comme un moyen pratique de calculer l’élancement d’un corps (nombre qui se doit d'être adimensionnel). Pour le prisme à base carrée, cet élancement p/4 redevient l’élancement L/c classique. Cette définition reste valable pour un corps quelconque (non prismatique, par exemple), le périmètre étant dans ce cas celui de la section frontale faisant face au mouvement comme pratiqué aux hauts Reynolds).
L'évasement en pavillon de trompette des courbes aux faibles élancements p/4 (c;-à-d. pour des corps de longueur L très courte) mériterait d'être étayé par de nouveaux calculs...
Il ne peut exister de prisme rectangulaire présentant un Cx linéaire (défini comme précisé) au dessus de la ligne noire marquée "1" et en-dessous de la ligne noire marquée "Infini".
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 16:15, 30 December 2018 |  | 1,181 × 579 (71 KB) | Bernard de Go Mars (talk | contribs) | Reverted to version as of 16:35, 27 December 2018 (UTC) |
| 16:36, 27 December 2018 |  | 959 × 466 (70 KB) | Bernard de Go Mars (talk | contribs) | Reverted to version as of 16:24, 27 December 2018 (UTC) | |
| 16:35, 27 December 2018 |  | 1,181 × 579 (71 KB) | Bernard de Go Mars (talk | contribs) | Reverted to version as of 11:48, 27 November 2018 (UTC) | |
| 16:24, 27 December 2018 |  | 959 × 466 (70 KB) | Bernard de Go Mars (talk | contribs) | Ajout du Cx linéaire de pression sur les faces frontales du prisme à base carrée (justification du recours de Bowen et Masliyah à un prisme à base carrée équivalent) | |
| 11:48, 27 November 2018 |  | 1,181 × 579 (71 KB) | Bernard de Go Mars (talk | contribs) | orthographe | |
| 11:08, 27 November 2018 |  | 1,181 × 579 (71 KB) | Bernard de Go Mars (talk | contribs) | Orthographe | |
| 11:02, 27 November 2018 |  | 1,181 × 579 (71 KB) | Bernard de Go Mars (talk | contribs) | User created page with UploadWizard |
You cannot overwrite this file.
File usage on Commons
There are no pages that use this file.
File usage on other wikis
The following other wikis use this file:
- Usage on fr.wikipedia.org
Metadata
This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.
| Horizontal resolution | 37.79 dpc |
|---|---|
| Vertical resolution | 37.79 dpc |